The Computational View of Time
Time is a central feature of human experience. But what actually is it? In traditional scientific accounts it’s often represented as some kind of coordinate much like space (though a coordinate that for some reason is always systematically increasing for us). But while this may be a useful mathematical description, it’s not telling us anything about what time in a sense “intrinsically is”.
We get closer as soon as we start thinking in computational terms. Because then it’s natural for us to think of successive states of the world as being computed one from the last by the progressive application of some computational rule. And this suggests that we can identify the progress of time with the “progressive doing of
But does this just mean that we are replacing a “time coordinate” with a “computational step count”? No. Because of the phenomenon of computational irreducibility. With the traditional mathematical idea of a time coordinate one typically imagines that this coordinate can be “set to any value”, and that then one can immediately calculate the state of the system at that time. But computational irreducibility implies that it’s not that easy. Because it says that there’s often essentially no better way to find what a system will do than by explicitly tracing through each step in its evolution.
In the pictures on the left there’s computational reducibility, and one can readily see what state will be after any number of steps t. But in the pictures on the right there’s (presumably) computational irreducibility, so that the only way to tell what will happen after t steps is effectively to run all those steps:
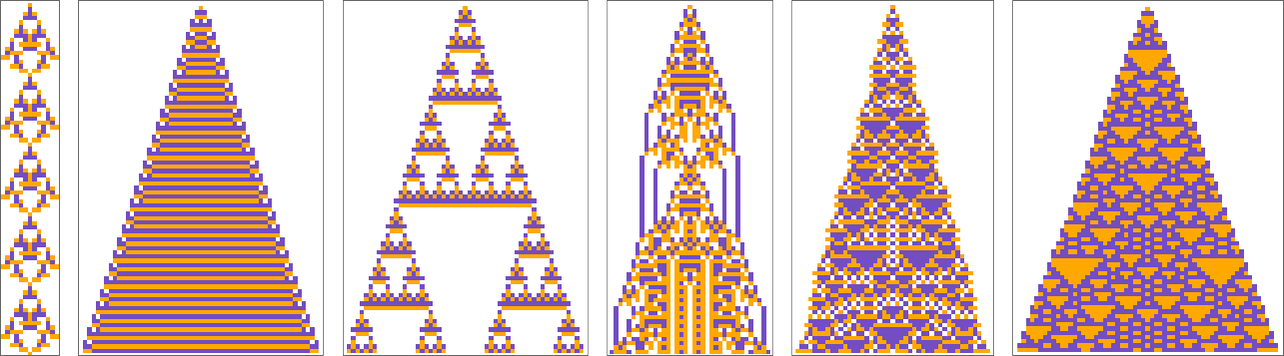
And this implies is that there’s a certain robustness to time when viewed in these computational terms. There’s no way to “jump ahead” in time; the only way to find out what will happen in the future is to go through the irreducible computational steps to get there.
There are simple idealized systems (say with purely periodic behavior) where there’s computational reducibility, and where there isn’t any robust notion of the progress of time. But the point is that—as the Principle of Computational Equivalence implies—our universe is inevitably full of computational irreducibility which in effect defines a robust notion of the progress of time.
The Role of the Observer
That time is a reflection of the progress of computation in the universe is an important starting point. But it’s not the end of the story. For example, here’s an immediate issue. If we have a computational rule that determines each successive state of a system it’s at least in principle possible to know the whole future of the system. So given this why then do we have the experience of the future only “unfolding as it happens”?
It’s fundamentally because of the way we are as observers. If the underlying system is computationally irreducible, then to work out its future behavior requires an irreducible amount of computational work. But it’s a core feature of observers like us that we are computationally bounded. So we can’t do all that irreducible computational work to “know the whole future”—and instead we’re effectively stuck just doing computation alongside the system itself, never able to substantially “jump ahead”, and only able to see the future “progressively unfold”.
In essence, therefore, we experience time because of the interplay between our computational boundedness as observers, and the computational irreducibility of underlying processes in the universe. If we were not computationally bounded, we could “perceive the whole of the future in one gulp” and we wouldn’t need a notion of time at all. And if there wasn’t underlying computational irreducibility there wouldn’t be the kind of “progressive revealing of the future” that we associate with our experience of time.
A notable feature of our everyday perception of time is that it seems to “flow only in one direction”—so that for example it’s generally much easier to remember the past than to predict the future. And this is closely related to the Second Law of thermodynamics, which (as I’ve argued at length elsewhere) is once again a result of the interplay between underlying computational irreducibility and our computational boundedness. Yes, the microscopic laws of physics may be reversible (and indeed if our system is simple—and computationally reducible—enough of this reversibility may “shine through”). But the point is that computational irreducibility is in a sense a much stronger force.
Imagine that we prepare a state to have orderly structure. If its evolution is computationally irreducible then this structure will effectively be “encrypted” to the point where a computationally bounded observer can’t recognize the structure. Given underlying reversibility, the structure is in some sense inevitably “still there”—but it can’t be “accessed” by a computationally bounded observer. And as a result such an observer will perceive a definite flow from orderliness in what is prepared to disorderliness in what is observed. (In principle one might think it should be possible to set up a state that will “behave antithermodynamically”—but the point is that to do so would require predicting a computationally irreducible process, which a computationally bounded observer can’t do.)
One of the longstanding confusions about the nature of time has to do with its “mathematical similarity” to space. And indeed ever since the early days of relativity theory it’s seemed convenient to talk about “spacetime” in which notions of space and time are bundled together.
But in our Physics Project that’s not at all how things fundamentally work. At the lowest level the state of the universe is represented by a hypergraph which captures what can be thought of as the “spatial relations” between discrete “atoms of space”. Time then corresponds to the progressive rewriting of this hypergraph.
And in a sense the “atoms of time” are the elementary “rewriting events” that occur. If the “output” from one event is needed to provide “input” to another, then we can think of the first event as preceding the second event in time—and the events as being “timelike separated”. And in general we can construct a causal graph that shows the dependencies between different events.
So how does this relate to time—and spacetime? As we’ll discuss below, our everyday experience of time is that it follows a single thread. And so we tend to want to “parse” the causal graph of elementary events into a series of slices that we can view as corresponding to “successive times”. As in standard relativity theory, there typically isn’t a unique way to assign a sequence of such “simultaneity surfaces”, with the result that there are different “reference frames” in which the identifications of space and time are different.
The complete causal graph bundles together what we usually think of as space with what we usually think of as time. But ultimately the progress of time is always associated with some choice of successive events that “computationally build on each other”. And, yes, it’s more complicated because of the possibilities of different choices. But the basic idea of the progress of time as “the doing of computation” is very much the same. (In a sense time represents “computational progress” in the universe, while space represents the “layout of its data structure”.)
Very much as in the derivation of the Second Law (or of fluid mechanics from molecular dynamics), the derivation of Einstein’s equations for the large-scale behavior of spacetime from the underlying causal graph of hypergraph rewriting depends on the fact that we are computationally bounded observers. But even though we’re computationally bounded, we still have to “have something going on inside”, or we wouldn’t record—or sense—any “progress in time”.
It seems to be the essence of observers like us—as captured in my recent Observer Theory—that we equivalence many different states of the world to derive our internal perception of “what’s going on outside”. And at some rough level we might imagine that we’re sensing time passing by the rate at which we add to those internal perceptions. If we’re not adding to the perceptions, then in effect time will stop for us—as happens if we’re asleep, anesthetized or dead.
It’s worth mentioning that in some extreme situations it’s not the internal structure of the observer that makes perceived time stop; instead it’s the underlying structure of the universe itself. As we’ve mentioned, the “progress of the universe” is associated with successive rewriting of the underlying hypergraph. But when there’s been “too much activity in the hypergraph” (which physically corresponds roughly to too much energy-momentum), one can end up with a situation in which “there are no more rewrites that can be done”—so that in effect some part of the universe can no longer progress, and “time stops” there. It’s analogous to what happens at a spacelike singularity (normally associated with a black hole) in traditional general relativity. But now it has a very direct computational interpretation: one’s reached a “fixed point” at which there’s no more computation to do. And so there’s no progress to make in time.
Multiple Threads of Time
Our strong human experience is that time progresses as a single thread. But now our Physics Project suggests that at an underlying level time is actually in effect multithreaded, or, in other words, that there are many different “paths of history” that the universe follows. And it is only because of the way we as observers sample things that we experience time as a single thread.
At the level of a particular underlying hypergraph the point is that there may be many different updating events that can occur, and each sequence of such updating event defines a different “path of history”. We can summarize all these paths of history in a multiway graph in which we merge identical states that arise:
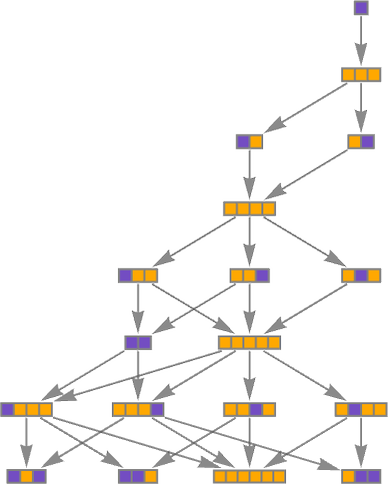
But given this underlying structure, why is it that we as observers believe that time progresses as a single thread? It all has to do with the notion of branchial space, and our presence within branchial space. The presence of many paths of history is what leads to quantum mechanics; the fact that we as observers ultimately perceive just one path is associated with the traditionally-quite-mysterious phenomenon of “measurement” in quantum mechanics.
When we talked about causal graphs above, we said that we could “parse” them as a series of “spacelike” slices corresponding to instantaneous “states of space”—represented by spatial hypergraphs. And by analogy we can similarly imagine breaking multiway graphs into “instantaneous slices”. But now these slices don’t represent states of ordinary space; instead they represent states of what we call branchial space.
Ordinary space is “knitted together” by updating events that have causal effects on other events that can be thought of as “located at different places in space”. (Or, said differently, space is knitted together by the overlaps of the elementary light cones of different events.) Now we can think of branchial space as being “knitted together” by updating events that have effects on events that end up on different branches of history.
(In general there is a close analogy between ordinary space and branchial space, and we can define a multiway causal graph that includes both “spacelike” and “branchlike” directions—with the branchlike direction supporting not light cones but what we can call entanglement cones.)
So how do we as observers parse what’s going on? A key point is that we are inevitably part of the system we’re observing. So the branching (and merging) that’s going on in the system at large is also going on in us. So that means we have to ask how a “branching mind” will perceive a branching universe. Underneath, there are lots of branches, and lots of “threads of history”. And there’s lots of computational irreducibility (and even what we can call multicomputational irreducibility). But computationally bounded observers like us have to equivalence most of those details to wind up with something that “fits in our finite minds”.
We can make an analogy to what happens in a gas. Underneath, there are lots of molecules bouncing around (and behaving in computationally irreducible ways). But observers like us are big compared to molecules, and (being computationally bounded) we don’t get to perceive their individual behavior, but only their aggregate behavior—from which we extract a thin set of computationally reducible “fluid-dynamics-level” features.
And it’s basically the same story with the underlying structure of space. Underneath, there’s an elaborately changing network of discrete atoms of space. But as large, computationally bounded observers we can only sample aggregate features in which many details have been equivalenced, and in which space tends to seem continuous and describable in basically computationally reducible ways.
So what about branchial space? Well, it’s basically the same story. Our minds are “big”, in the sense that they span many individual branches of history. And they’re computationally bounded so they can’t perceive the details of all those branches, but only certain aggregated features. And in a first approximation what then emerges is in effect a single aggregated thread of history.
With sufficiently careful measurements we can sometimes see “quantum effects” in which multiple threads of history are in evidence. But at a direct human level we always seem to aggregate things to the point where what we perceive is just a single thread of history—or in effect a single thread of progression in time.
It’s not immediately obvious that any of these “aggregations” will work. It could be that important effects we perceive in gases would depend on phenomena at the level of individual molecules. Or that to understand the large-scale structure of space we’d continually be having to think about detailed features of atoms of space. Or, similarly, that we’d never be able to maintain a “consistent view of history”, and that instead we’d always be having to trace lots of individual threads of history.
But the key point is that for us to stay as computationally bounded observers we have to pick out only features that are computationally reducible—or in effect boundedly simple to describe.
Closely related to our computational boundedness is the important assumption we make that we as observers have a certain persistence. At every moment in time, we are made from different atoms of space and different branches in the multiway graph. Yet we believe we are still “the same us”. And the crucial physical fact (that has to be derived in our model) is that in ordinary circumstances there’s no inconsistency in doing this.
So the result is that even though there are many “threads of time” at the lowest level—representing many different “quantum branches”—observers like us can (usually) successfully still view there as being a single consistent perceived thread of time.
But there’s another issue here. It’s one thing to say that a single observer (say a single human mind or a single measuring device) can perceive history to follow a single, consistent thread. But what about different human minds, or different measuring devices? Why should they perceive any kind of consistent “objective reality”?
Essentially the answer, I think, is that they’re all sufficiently nearby in branchial space. If we think about physical space, observers in different parts of the universe will clearly “see different things happening”. The “laws of physics” may be the same—but what star (if any) is nearby will be different. Yet (at least for the foreseeable future) for all of us humans it’s always the same star that’s nearby.
And so it is, presumably, in branchial space. There’s some small patch in which we humans—with our shared origins—exist. And it’s presumably because that patch is small relative to all of branchial space that all of us perceive a consistent thread of history and a common objective reality.
There are many subtleties to this, many of which aren’t yet fully worked out. In physical space, we know that effects can in principle spread at the speed of light. And in branchial space the analog is that effects can spread at the maximum entanglement speed (whose value we don’t know, though it’s related by Planck unit conversions to the elementary length and elementary time). But in maintaining our shared “objective” view of the universe it’s crucial that we’re not all going off in different directions at the speed of light. And of course the reason that doesn’t happen is that we don’t have zero mass. And indeed presumably nonzero mass is a critical part of being observers like us.
In our Physics Project it’s roughly the density of events in the hypergraph that determines the density of energy (and mass) in physical space (with their associated gravitational effects). And similarly it’s roughly the density of events in the multiway graph (or in branchial graph slices) that determines the density of action—the relativistically invariant analog of energy—in branchial space (with its associated effects on quantum phase). And though it’s not yet completely clear how this works, it seems likely that once again when there’s mass, effects don’t just “go off at the maximum entanglement speed in all directions”, but instead stay nearby.
There are definitely connections between “staying at the same place”, believing one is persistent, and being computationally bounded. But these are what seem necessary for us to have our typical view of time as a single thread. In principle we can imagine observers very different from us—say with minds (like the inside of an idealized quantum computer) capable of experiencing many different threads of history. But the Principle of Computational Equivalence suggests that there’s a high bar for such observers. They need not only to be able to deal with computational irreducibility but also multicomputational irreducibility, in which one includes both the process of computing new states, and the process of equivalencing states.
And so for observers that are “anything like us” we can expect that once again time will tend to be as we normally experience it, following a single thread, consistent between observers.
(It’s worth mentioning that all of this only works for observers like us “in situations like ours”. For example, at the “entanglement horizon” for a black hole—where branchially-oriented edges in the multiway causal graph get “trapped”—time as we know it in some sense “disintegrates”, because an observer won’t be able to “knit together” the different branches of history to “form a consistent classical thought” about what happens.)
Time in the Ruliad
In what we’ve discussed so far we can think of the progress of time as being associated with the repeated application of rules that progressively “rewrite the state of the universe”. In the previous section we saw that these rules can be applied in many different ways, leading to many different underlying threads of history.
But so far we’ve imagined that the rules that get applied are always the same—leaving us with the mystery of “Why those rules, and not others?” But this is where the ruliad comes in. Because the ruliad involves no such seemingly arbitrary choices: it’s what you get by following all possible computational rules.
One can imagine many bases for the ruliad. One can make it from all possible hypergraph rewritings. Or all possible (multiway) Turing machines. But in the end it’s a single, unique thing: the entangled limit of all possible computational processes. There’s a sense in which “everything can happen somewhere” in the ruliad. But what gives the ruliad structure is that there’s a definite (essentially geometrical) way in which all those different things that can happen are arranged and connected.
So what is our perception of the ruliad? Inevitably we’re part of the ruliad—so we’re observing it “from the inside”. But the crucial point is that what we perceive about it depends on what we are like as observers. And my big surprise in the past few years has been that assuming even just a little about what we’re like as observers immediately implies that what we perceive of the ruliad follows the core laws of physics we know. In other words, by assuming what we’re like as observers, we can in effect derive our laws of physics.
The key to all this is the interplay between the computational irreducibility of underlying behavior in the ruliad, and our computational boundedness as observers (together with our related assumption of our persistence). And it’s this interplay that gives us the Second Law in statistical mechanics, the Einstein equations for the structure of spacetime, and (we think) the path integral in quantum mechanics. In effect what’s happening is that our computational boundedness as observers makes us equivalence things to the point where we are sampling only computationally reducible slices of the ruliad, whose characteristics can be described using recognizable laws of physics.
So where does time fit into all of this? A central feature of the ruliad is that it’s unique—and everything about it is “abstractly necessary”. Much as given the definition of numbers, addition and equality it’s inevitable that one gets 1 + 1 = 2, so similarly given the definition of computation it’s inevitable that one gets the ruliad. Or, in other words, there’s no question about whether the ruliad exists; it’s just an abstract construct that inevitably follows from abstract definitions.
And so at some level this means that the ruliad inevitably just “exists as a complete thing”. And so if one could “view it from outside” one could think of it as just a single timeless object, with no notion of time.
But the crucial point is that we don’t get to “view it from the outside”. We’re embedded within it. And, what’s more, we must view it through the “lens” of our computational boundedness. And this is why we inevitably end up with a notion of time.
We observe the ruliad from some point within it. If we were not computationally bounded then we could immediately compute what the whole ruliad is like. But in actuality we can only discover the ruliad “one computationally bounded step at a time”—in effect progressively applying bounded computations to “move through rulial space”.
So even though in some abstract sense “the whole ruliad is already there” we only get to explore it step by step. And that’s what gives us our notion of time, through which we “progress”.
Inevitably, there are many different paths that we could follow through the ruliad. And indeed every mind (and every observer like us)—with its distinct inner experience—presumably follows a different path. But much as we described for branchial space, the reason we have a shared notion of “objective reality” is presumably that we are all very close together in rulial space; we form in a sense a tight “rulial flock”.
It’s worth pointing out that not every sampling of the ruliad that may be accessible to us conveniently corresponds to exploration of progressive slices of time. Yes, that kind of “progression in time” is characteristic of our physical experience, and our typical way of describing it. But what about our experience, say, of mathematics?
The first point to make is that just as the ruliad contains all possible physics, it also contains all possible mathematics. If we construct the ruliad, say from hypergraphs, the nodes are now not “atoms of space”, but instead abstract elements (that in general we call emes) that form pieces of mathematical expressions and mathematical theorems. We can think of these abstract elements as being laid out now not in physical space, but in some abstract metamathematical space.
In our physical experience, we tend to remain localized in physical space, branchial space, etc. But in “doing mathematics” it’s more as if we’re progressively expanding in metamathematical space, carving out some domain of “theorems we assume are true”. And while we could identify some kind of “path of expansion” to let us define some analog of time, it’s not a necessary feature of the way we explore the ruliad.
Different places in the ruliad in a sense correspond to describing things using different rules. And by analogy to the concept of motion in physical space, we can effectively “move” from one place to another in the ruliad by translating the computations done by one set of rules to computations done by another. (And, yes, it’s nontrivial to even have the possibility of “pure motion”.) But if we indeed remain localized in the ruliad (and can maintain what we can think of as our “coherent identity”) then it’s natural to think of there being a “path of motion” along which we progress “with time”. But when we’re just “expanding our horizons” to encompass more paradigms and to bring more of rulial space into what’s covered by our minds (so that in effect we’re “expanding in rulial space”), it’s not really the same story. We’re not thinking of ourselves as “doing computation in order to move”. Instead, we’re just identifying equivalences and using them to expand our definition of ourselves, which is something that we can at least approximate (much like in “quantum measurement” in traditional physics) as happening “outside of time”. Ultimately, though, everything that happens must be the result of computations that occur. It’s just that we don’t usually “package” these into what we can describe as a definite thread of time.
So What in the End Is Time?
From the paradigm (and Physics Project ideas) that we’ve discussed here, the question “What is time?” is at some level simple: time is what progresses when one applies computational rules. But what’s critical is that time can in effect be defined abstractly, independent of the details of those rules, or the “substrate” to which they’re applied. And what makes this possible is the Principle of Computational Equivalence, and the ubiquitous phenomenon of computational irreducibility that it implies.
To begin with, the fact that time can robustly be thought of as “progressing”, in effect in a linear chain, is a consequence of computational irreducibility—because computational irreducibility is what tells us that computationally bounded observers like us can’t in general ever “jump ahead”; we just have to follow a linear chain of steps.
But there’s something else as well. The Principle of Computational Equivalence implies that there’s in a sense just one (ubiquitous) kind of computational irreducibility. So when we look at different systems following different irreducible computational rules, there’s inevitably a certain universality to what they do. In effect they’re all “accumulating computational effects” in the same way. Or in essence progressing through time in the same way.
There’s a close analogy here with heat. It could be that there’d be detailed molecular motion that even on a large scale worked noticeably differently in different materials. But the fact is that we end up being able to characterize any such motion just by saying that it represents a certain amount of heat, without getting into more details. And that’s very much the same kind of thing as being able to say that such-and-such an amount of time has passed, without having to get into the details of how some clock or other system that reflects the passage of time actually works.
And in fact there’s more than a “conceptual analogy” here. Because the phenomenon of heat is again a consequence of computational irreducibility. And the fact that there’s a uniform, “abstract” characterization of it is a consequence of the universality of computational irreducibility.
It’s worth emphasizing again, though, that just as with heat, a robust concept of time depends on us being computationally bounded observers. If we were not, then we’d able to break the Second Law by doing detailed computations of molecular processes, and we wouldn’t just describe things in terms of randomness and heat. And similarly, we’d be able to break the linear flow of time, either jumping ahead or following different threads of time.
But as computationally bounded observers of computationally irreducible processes, it’s basically inevitable that—at least to a good approximation—we’ll view time as something that forms a single one-dimensional thread.
In traditional mathematically based science there’s often a feeling that the goal should be to “predict the future”—or in effect to “outrun time”. But computational irreducibility tells us that in general we can’t do this, and that the only way to find out what will happen is just to run the same computation as the system itself, essentially step by step. But while this might seem like a letdown for the power of science, we can also see it as what gives meaning and significance to time. If we could always jump ahead then at some level nothing would ever fundamentally be achieved by the passage of time (or, say, by the living of our lives); we’d always be able to just say what will happen, without “living through” how we got there. But computational irreducibility gives time and the process of it passing a kind of hard, tangible character.
So what does all this imply for the various classic issues (and apparent paradoxes) that arise in the way time is usually discussed?
Let’s start with the question of reversibility. The traditional laws of physics basically apply both forwards and backwards in time. And the ruliad is inevitably symmetrical between “forward” and “backward” rules. So why is it then that in our typical experience time always seems to “run in the same direction”?
This is closely related to the Second Law, and once again it’s consequence of our computational boundedness interacting with underlying computational irreducibility. In a sense what defines the direction of time for us is that we (typically) find it much easier to remember the past than to predict the future. Of course, we don’t remember every detail of the past. We only remember what amounts to certain “filtered” features that “fit in our finite minds”. And when it comes to predicting the future, we’re limited by our inability to “outrun” computational irreducibility.
Let’s recall how the Second Law works. It basically says that if we set up some state that’s “ordered” or “simple” then this will tend to “degrade” to one that’s “disordered” or “random”. (We can think of the evolution of the system as effectively “encrypting” the specification of our starting state to the point where we—as computationally bounded observers—can no longer recognize its ordered origins.) But because our underlying laws are reversible, this degradation (or “encryption”) must happen when we go both forwards and backwards in time:

But the point is that our “experiential” definition of the direction of time (in which the “past” is what we remember, and the “future” is what we find hard to predict) is inevitably aligned with the “thermodynamic” direction of time we observe in the world at large. And the reason is that in both cases we’re defining the past to be something that’s computationally bounded (while the future can be computationally irreducible). In the experiential case the past is computationally bounded because that’s what we can remember. In the thermodynamic case it’s computationally bounded because those are the states we can prepare. In other words, the “arrows of time” are aligned because in both cases we are in effect “requiring the past to be simpler”.
So what about time travel? It’s a concept that seems natural—and perhaps even inevitable—if one imagines that “time is just like space”. But it becomes a lot less natural when we think of time in the way we’re doing here: as a process of applying computational rules.
Indeed, at the lowest level, these rules are by definition just sequentially applied, producing one state after another—and in effect “progressing in one direction through time”. But things get more complicated if we consider not just the raw, lowest-level rules, but what we might actually observe of their effects. For example, what if the rules lead to a state that’s identical to one they’ve produced before (as happens, for example, in a system with periodic behavior)? If we equivalence the state now and the state before (so we represent both as a single state) then we can end up with a loop in our causal graph (a “closed timelike curve”). And, yes, in terms of the raw sequence of applying rules these states can be considered different. But the point is that if they are identical in every feature then any observer will inevitably consider them the same.
But will such equivalent states ever actually occur? As soon as there’s computational irreducibility it’s basically inevitable that the states will never perfectly match up. And indeed for the states to contain an observer like us (with “memory”, etc.) it’s basically impossible that they can match up.
But can one imagine an observer (or a “timecraft”) that would lead to states that match up? Perhaps somehow it could carefully pick particular sequences of atoms of space (or elementary events) that would lead it to states that have “happened before”. And indeed in a computationally simple system this might be possible. But as soon as there’s computational irreducibility, this simply isn’t something one can expect any computationally bounded observer to be able to do. And, yes, this is directly analogous to why one can’t have a “Maxwell’s demon” observer that “breaks the Second Law”. Or why one can’t have something that carefully navigates the lowest-level structure of space to effectively travel faster than light.
But even if there can’t be time travel in which “time for an observer goes backwards”, there can still be changes in “perceived time”, say as a result of relativistic effects associated with motion. For example, one classic relativistic effect is time dilation, in which “time goes slower” when objects go faster. And, yes, given certain assumptions, there’s a straightforward mathematical derivation of this effect. But in our effort to understand the nature of time we’re led to ask what its physical mechanism might be. And it turns out that in our Physics Project it has a surprisingly direct—and almost “mechanical”—explanation.
One starts from the fact that in our Physics Project space and everything in it is represented by a hypergraph which is continually getting rewritten. And the evolution of any object through time is then defined by these rewritings. But if the object moves, then in effect it has to be “re-created at a different place in space”—and this process takes up a certain number of rewritings, leaving fewer for the intrinsic evolution of the object itself, and thus causing time to effectively “run slower” for it. (And, yes, while this is a qualitative description, one can make it quite formal and precise, and recover the usual formulas for relativistic time dilation.)
Something similar happens with gravitational fields. In our Physics Project, energy-momentum (and thus gravity) is effectively associated with greater activity in the underlying hypergraph. And the presence of this greater activity leads to more rewritings, causing “time to run faster” for any object in that region of space (corresponding to the traditional “gravitational redshift”).
More extreme versions of this occur in the context of black holes. (Indeed, one can roughly think of spacelike singularities as places where “time ran so fast that it ended”.) And in general—as we discussed above—there are many “relativistic effects” in which notions of space and time get mixed in various ways.
But even at a much more mundane level there’s a certain crucial relationship between space and time for observers like us. The key point is that observers like us tend to “parse” the world into a sequence of “states of space” at successive “moments in time”. But the fact that we do this depends on some quite specific features of us, and in particular our effective physical scale in space as compared to time.
In our everyday life we’re typically looking at scenes involving objects that are perhaps tens of meters away from us. And given the speed of light that means photons from these objects get to us in less than a microsecond. But it takes our brains milliseconds to register what we’ve seen. And this disparity of timescales is what leads us to view the world as consisting of a sequence of states of space at successive moments in time.
If our brains “ran” a million times faster (i.e. at the speed of digital electronics) we’d perceive photons arriving from different parts of a scene at different times, and we’d presumably no longer view the world in terms of overall states of space existing at successive times.
The same kind of thing would happen if we kept the speed of our brains the same, but dealt with scenes of a much larger scale (as we already do in dealing with spacecraft, astronomy, etc.).
But while this affects what it is that we think time is “acting on”, it doesn’t ultimately affect the nature of time itself. Time remains that computational process by which successive states of the world are produced. Computational irreducibility gives time a certain rigid character, at least for computationally bounded observers like us. And the Principle of Computational Equivalence allows there to be a robust notion of time independent of the “substrate” that’s involved: whether us as observers, the everyday physical world, or, for that matter, the whole universe.

